
Here, we want to construct a box and whisker plot
The first thing to do here is to arrange the data set in ascending order
We already have this done in the question as follows;
2,2,3,5,5,8,9,10,10,10,11,13,13
On the box plot, we have five points to plot; we have them as follows;
a) Minimum value
This is the lowest possible value in the dataset. According to the given dataset, the minimum value is 2.
b) First Quartile
The formula we use for the term which is the first quartile is as follows;
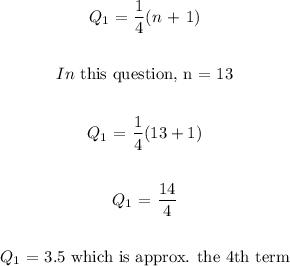
So what this mean is that the lower quartile is the 4th term which in this case is 5
c) Median
The median is the mid-value of the arranged dataset. If we count from any of the ends, the 7th term is the median
In this case, the median is 9
d) Third Quartile
The third quartile can be calculated using the mathematical formula below;

In this case, the 11th term is 11
e) Maximum value
This is the highest number in the data set which is 13
As we can see the layout on the question, we place the values above at each of the points in the manner in which they are answered accordingly;
The plot is shown below;