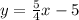Question

5. Elena wanted to find the slope and y-intercept of the graph of 25% - 20y = 100.She decided to put the equation in slope-intercept forrn first. Here is her work-25x – 20y = 10020y = 100 – 25x5y = 5 - -y=5.5- 5. Describe Elena's mistake in her work above, and what the correct slopeand y-intercept of the line are.What are the x- and y-intercepts of the equation 4y + 9x = 18?

Answer 1

The equation we have is:

`25x-20y=100`

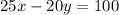
The correct way to solve this equation for y is:

`\begin{gathered} 25x-20y=100 \\ \text{Substract 25x to both sides:} \\ -20y=100-25x \\ \text{Divide both sides by -20} \\ y=(100)/(-20)-(25x)/(-20) \\ \text{simplify:} \\ y=-5+(5)/(4)x \end{gathered}`

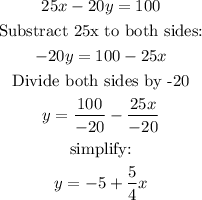
By comparing this process to the work from Elena, we can see that in her second step, she missed the negative sign:

the term 20y, must still be negative: -20y.

-----

The correct slope and y-intercept line:

From the process we did by solving for y, we can find the slope-intercept equation of the line.

Remember that the general slope-intercept equation is:

`y=mx+b`

Where m is the slope and b is the y-intercept.

When we solved correctly for y, our result was:

`y=-5+(5)/(4)x`

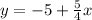
Representing this result in the slope-intercept form:

`y=(5)/(4)x-5`

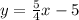
Where the slope is 5/4 and the y-intercept is -5.

Answer: Her mistake was that she missed the negative sign in the second step, and the correct slope-intercept equation is:

`y=(5)/(4)x-5`