Step 1: Draw the triangle.
Step 2: Concept
Use the trigonometric ratio to find the length of the string.
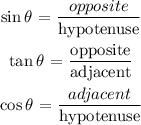
Step 3: Name the sides of the triangle
Hypotenuse = L side facing right angle
Opposite = 82 ft side facing given angle
Adjacent = ___ The third side.
Step 4: Apply the sine formula to find the length of the string.

Next, cross multiply
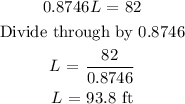
Final answer
The length of the string = 93.8 ft