Due to the total mechanical energy is conserved, you have that the potential energy of the cart at 140 m must be equal to the sum of the potential energy and kinetic energy of the cart at 95m.
Then, you can write:
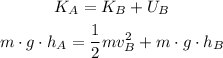
where
hA = 140m
hB = 95 m
g = 9.8 m/s^2
m = 950 kg
cancel out the mass m in the previous equation, and solve for vB:
![\begin{gathered} v_B=2g\cdot h_A-2g\cdot h_B \\ v_B=\sqrt[]{2((9.8m)/(s^2))(140m)-2((9.8m)/(s^2))(95m)} \\ v_B=29.7(m)/(s) \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/1j9bwzvr8wdeqppf8u5eo2ux3fgxnvb6lb.png)
Hence, when the cart reaches the point B, its speed is approximately 29.7 m/s