Question

67. Two sides of a triangle have lengths 8 and 17. Which expression describes the length of the third side?A. greater than 9 and at most 25C. at least 9 and at most 25B. at least 9 and less than 25D. greater than 9 and less than 25

Answer 1

One of the conditions for forming a triangle is:

The sum of the length of any two sides of a triangle is greater than the length of the third side.

i.e. if we have this triangle:

The condition means:

`\begin{gathered} a+b>c \\ OR \\ a+c>b \\ OR \\ b+c>a \end{gathered}`

Let us now apply this condition to the question.

I. If the third side is the largest side:

We have been given two sides with lengths 8 and 17.

Let us make a = 8 and b = 17 and c is the third side

Using the condition we have:

`\begin{gathered} a+b>c \\ a=8 \\ b=17 \\ 8+17>c \\ 25>c \\ \\ \text{Meaning that;} \\ c<25 \end{gathered}`

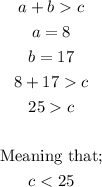
This implies that the length of the third side must be less than 25.

II. If the third side is the smallest side:

Again let us make a = 8 and c = 17 and b is the third side

Using the condition, we have:

`\begin{gathered} a+b>c \\ a=8 \\ c=17 \\ 8+b>17 \\ \\ \text{subtract 8 from both sides} \\ 8-8+b>17-8 \\ b>9 \end{gathered}`

This implies that the length of the third side must be greater than 9.

Therefore the answer is Option D