Question

A radar station at A is tracking ships at B and C. How far apart are the two ships?

Answer 1

Given:

There are given that the triangle ABC.

Where,

`\begin{gathered} AB=3.3km \\ AC=4.5km \\ \angle A=100^(\circ) \end{gathered}`

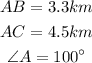
Step-by-step explanation:

According to the question:

We need to find the value for BC:

So,

To find the value of BC, we need to use the cosine rule:

From the cosine rule:

`BC^2=b^2+c^2-2bccosA`

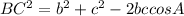
Then,

Put the all values into the given formula:

`\begin{gathered} BC^(2)=b^(2)+c^(2)-2bccosA \\ BC^2=(4.5)^2+(3.3)^2-2(4.5)(3.3)cos100^(\circ) \end{gathered}`

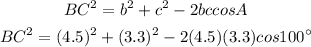
Then,

Then,

`\begin{gathered} BC^(2)=20.25+10.89-29.7(-0.17) \\ BC^2=20.25+10.89+5.049 \\ BC^2=36.189 \\ BC=6.016 \end{gathered}`

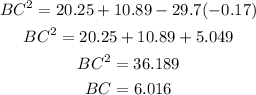
Final answer:

Hence, the value of BC is 6.016 km.