Question

Giver DABC ~0872, find the ratio and the missing sicles, 12 m 21m B Im А 모드 Z с C 근 SZ b Z 17.5m be Z-

Answer 1

b = 10.03, z= 12.25

1) Similar triangles have proportional sides and congruent angles. Therefore we can write out the following ratios:

`\begin{gathered} (BC)/(YZ)=(CA)/(XZ) \\ (12)/(21)=(b)/(17.5) \\ 21b=12\cdot17.5 \\ (21b)/(21)=(12)/(21)\cdot(17.5)/(21) \\ b=10.03 \end{gathered}`

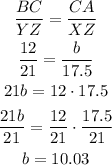
2) And for the other missing side, we can write out this proportion:

`\begin{gathered} (BC)/(AB)=(ZY)/(XY) \\ (12)/(7)=(21)/(z) \\ 12z=7\cdot21 \\ (12z)/(12)=(7\cdot21)/(12) \\ z=12.25 \end{gathered}`

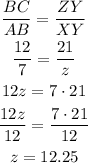
3) Hence, the missing sides are b = 10.03 (rounded off to the nearest hundredth) and z= 12.25