Question

given:• Square WJTSquare CBAZW is the midpoint of segment CZ• The perimeter of square WVJT is 12V2.BwThe measure of angle VWT isThe measure of angle CWV isThe length .cw isThe perimeter of square CBAZ is

Answer 1

All four interior angles of a square are 90°

Therefore,

The measure of ∠VWT will be

`\angle VWT=90^0`

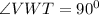
Hence,

∠VWT = 90°

Step2:measure the angle CWV

Sum of angles in a triangle is

`=180^0`

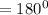
Therefore,

`\begin{gathered} \angle CWV+\angle CVW+WCV=180^0 \\ \theta+\theta+90^0=180^0(isosceles\text{ triangle)} \\ 2\theta=180^0-90^0 \\ 2\theta=90^0 \\ \text{Divide both sides by 2} \\ (2\theta)/(2)=(90^0)/(2) \\ \theta=45^0 \end{gathered}`

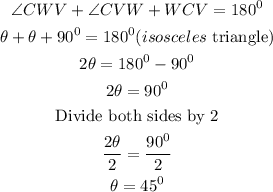
Hence,

∠ CWV = 45°

Since the perimeter of the square WVJT

`=12\sqrt[]{2}`

Then

`VW+WT+TJ+JV=12\sqrt[]{2}`

All sides of a square are equal, therefore,

`VW=WT=TJ=JV=x`

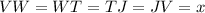
Hence, we will have that

`\begin{gathered} x+x+x+x=12\sqrt[]{2} \\ 4x=12\sqrt[]{2} \\ \text{divide both sides by 4} \\ (4x)/(4)=\frac{12\sqrt[]{2\text{ }}}{4} \\ x=3\sqrt[]{2} \end{gathered}`
`\begin{gathered} CW=y=\text{ADJACENT} \\ CV=y=\text{OPPOSITE} \\ VW=3\sqrt[]{2}=\text{HYPOTENUS} \end{gathered}`

Using the Pythagoras theorem,we will have

`\begin{gathered} \text{hypotenus}^2=\text{opposite}^2+\text{adjacent}^2 \\ (3\sqrt[]{2)}^2=y^2+y^2 \\ 2y^2=9*2 \\ 2y^2=18 \\ \text{diveide both sides by 2} \\ (2y^2)/(2)=(18)/(2) \\ y^2=9 \\ \text{squareroot both sides } \\ y=\sqrt[]{9} \\ y=3 \end{gathered}`

Therefore,

Length CW = 3

The perimeter of CBAZ IS

`\text{PERIMTER}=\text{ CB+BA+AZ+ZC}`
`\begin{gathered} ZC=CW+ZW \\ \text{But CW=ZW=3} \\ \text{Therefore} \\ ZC=3+3 \\ ZC=6 \end{gathered}`

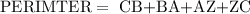
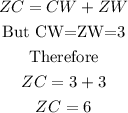
Recall, that all sides of a square are equal,

Hence,

`ZC=CB=BA=AZ=6`

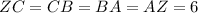
Therefore, perimeter of CBAZ will be

`\begin{gathered} \text{Perimeter of CBAZ=6+6+6+6} \\ \text{PERIMETER =24} \end{gathered}`

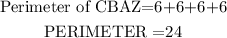
Hence,

Perimeter of CBAZ =24