Question

Express your answer as a fraction in lowest terms or a decimal rounded to the nearest millionth

Answer 1

The probability of obtaining exactly 7 heads when flipping 8 coins can be deduced using the binomial probability

The formula for the binomial probability, P, is

`P_x=(^n_x)p^xq^(n-x)`

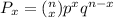
Where

`\begin{gathered} n=8 \\ x=7 \\ p=(1)/(2) \\ q=1-p=1-(1)/(2)=(1)/(2) \\ \text{Bceause when you flip a coin, you either get a head or a tail} \\ \text{Thus the proability of getting a head or tail i.e p or q is }(1)/(2) \end{gathered}`

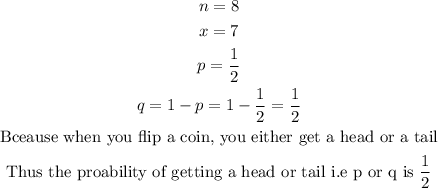
Substitute the values into the formula for binomial probability

`\begin{gathered} P_x=(^n_x)p^xq^(n-x) \\ P_7=^8C_7*((1)/(2))^7*((1)/(2))^(8-7)_{} \\ P_7=8*(1)/(128)*(1)/(2)=(8)/(256)=(1)/(32) \\ P_7=(1)/(32) \end{gathered}`

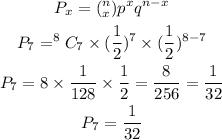
Hence, the probability of obtaining exactly 7 heads when flipping 8 coins is 1/32 (in fractions)