Question

Question: For #1-3, write the equation of the following lines 1. ** 3 2 1 3 x 2 3 4

Answer 1

The two points on the line is (0,-1) and (3,-6).

Use the slope intersept form to calculate the equation of the line.

`y-y1=(y2-y1)/(x2-x1)(x-x1)`

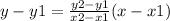
Put these points in the equation implies,

`\begin{gathered} y+1=(-6+1)/(3-0)(x-0) \\ y+1=(-5)/(3)x \\ 3y+3=-5x \\ 3y+5x+3=0 \end{gathered}`

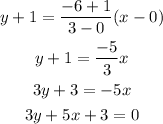
Therefore, the equation of the line is 3y+5x+3=0.

Consider the second line, the points are (0,-2) and (1,0).

`\begin{gathered} y+2=(0+2)/(1-0)x \\ y+2=2x \\ y=2x-2 \end{gathered}`

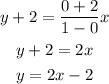
Thus, the equation of the line is y=2x-2.

Consider the third line, the points are (0,1) and (-3,6).

`\begin{gathered} y-1=(6-1)/(-3-0)x \\ y-1=-(5)/(3)x \\ y=-(5)/(3)x+1 \end{gathered}`

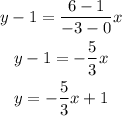
Thus, the equation of the line is y=-(5/3)x+1.