Question

The digit sum of a three-digit number is 10. If we reverse the digits, we get a smaller number. If we divide the original number by this smaller number, we get a quotient of 3 and a remainder of 178. The hundreds digits is four times the units digit. Determine the original number.

Answer 1

Let the three-digit number be

`=xyz`

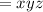
The sum of the three digits will be

`x+y+z=10\ldots\ldots\ldots\ldots\ldots\text{.}.(1)`

The original digits will be

`100x+10y+z\ldots\ldots\ldots\ldots\text{.}(2)`

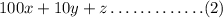
By reversing the digits we will have (smaller number)

`100z+10y+x\ldots\ldots\ldots\ldots\text{.}(3)`

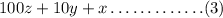
If a hundred digits is x, then the unit digit will be

`\begin{gathered} x=4* z \\ x=4z\ldots\ldots\text{.}\ldots\ldots(4) \end{gathered}`

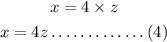
If we dive the original number by the smaller number we will have a quotient of 3 and a remainder of 178, we will have

`\begin{gathered} (100x+10y+z)/(100z+10y+x)=3(178)/(100z+10y+x) \\ \text{that is} \\ 100x+10y+z=3(100z+10y+x)+178 \\ 100x+10y+z=300z+30y+3x+178 \\ 100x-3x+10y-30y+z-300z=178 \\ 97x-20y-299z=178\ldots\ldots\ldots(5) \end{gathered}`

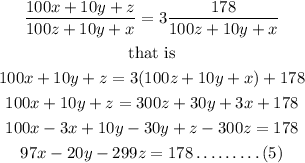
lets substitute equation (4) in equation (1)

`\begin{gathered} x+y+z=10 \\ 4z+y+z=10 \\ 5z+y=10\ldots\ldots\ldots\ldots(6) \end{gathered}`

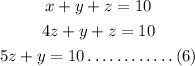
lets substitute equation (4) in equation (5)

`\begin{gathered} 97x-20y-299z=178 \\ 97(4z)-20y-299z=178 \\ 388z-20y-299z=178 \\ 388z-299z-20y=178 \\ 89z-20y=178\ldots\ldots\ldots\ldots(7) \end{gathered}`

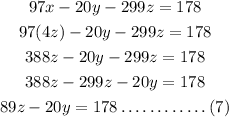
combining equations (6) and (7) and solving simultaneously, we will have

`\begin{gathered} 5z+y=10 \\ 89z-20y=178 \\ \text{fom equation (6) we will have that} \\ y=10-5z\ldots\ldots\ldots\text{.}(8) \end{gathered}`

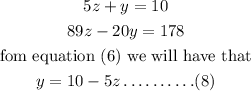
Substitute equation (8) in equation 7, we will have

`\begin{gathered} 89z-20(10-5z)=178 \\ 89z-200+100z=178 \\ 89z+100z=178+200 \\ 189z=378 \\ (189z)/(189)=(378)/(189) \\ z=2 \end{gathered}`

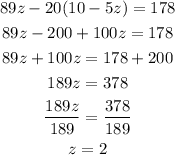
substitute z=2 in equation (8)

`\begin{gathered} y=10-5z \\ y=10-5(2) \\ y=10-10 \\ y=0 \end{gathered}`

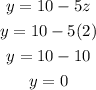
Recall equation (4)

`\begin{gathered} x=4z \\ x=4(2) \\ x=8 \end{gathered}`

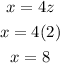
SINCE THE ORIGINAL NUMBER IS

`\begin{gathered} =100x+10y+z \\ =100(8)+10(0)+2 \\ =800+0+2 \\ =802 \end{gathered}`

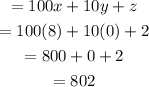
Hence,

The original number is = 802