Question

I got the 2nd , 5th, and 6th question right but I cant figure out the others

Answer 1

For this problem, we are given a normal distribution that has a mean equal to $1800 and a standard deviation of $135. We need to calculate a few percentages based on this information.

The first one is the approximate percentage of buyers who paid more than 2070.

In order to solve this, we need to find the z-score, which is given by the following formula:

`z=(x-\mu)/(\sigma)`

Where "x" is the desired value, "mi" is the mean, and "sigma" is the standard deviation. For this case we have:

`z=(2070-1800)/(135)=2`

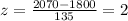
The z-score is equal to 2. Now we need to go on the z-table where we will find the percentage of everyone that paid less than 2070, this is not the value we want, but we can subtract this value from 1 to determine what we want. This is shown below:

`P(z>2)=1-P(z<2)=1-0.9772=0.02275`

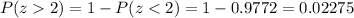
The percentage is 2.275%

Now we need to find the percentage of buyers who paid between 1800 and 2205. For this we need to find the z-score for both values:

`\begin{gathered} z_1=(1800-1800)/(135)=0 \\ z_2=(2205-1800)/(135)=3 \end{gathered}`

To solve this item, we need to go on the z-table and find the percentage for both. Then we need to subtract the P(z<3) with P(z<0).

`P(0<strong>The percentage is 49.87%</strong><p>Now we need to calculate the values between 1800 and 2070. We already found the score for 1800 and the one for 2070, so we can subtract the percentages directly:</p>[tex]P(0<strong>The percentage is 47.72%</strong><p>Now we need to calculate the percentage that paid less than $1395. We need to find the z-score for this value:</p>[tex]z=(1395-1800)/(135)=-3`

Now we need to find the value that corresponds to -3 on the z-table:

`P(z<-3)=0.0013`

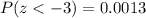
The percentage is 0.13%

Now we need to find the percentage of buyers who paid between $1665 and $1800. We already have the percentage for those who paid less than $1800, now we need to calculate the z-score of $1665.

`z=(1665-1800)/(135)=-1`

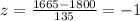
The percentage is:

[tex]P(-1The percentage is 34.13%