The figure given is a circle with two tangents meeting at point M and touching the circle at points L and N.
The angle made by the arc is 138 degrees
In order to get a better understanding, we can redraw the figure.
This is done below:
As we can see, the angle subtended by the arc LN, is 138 degrees.
There is a theorem that says the angle that a radius (such as OL) makes with a tangent
(such as LM) is 90 degrees.
This is illustrated further below:
This new image highlights the 90 degree angles the two tangents make with the radius of the circle.
Thus, we can consider quadrilateral MNOL, we can finally solve for x.
A theorem says that the sum of angles in a quadrilateral is 360 degrees.
Therefore, we can say:
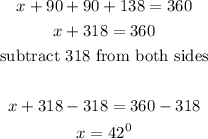
Therefore the final answer is: x = 42 degrees