Question

Choose two ordered pairs from the graph and find the ratio of y and x to calculate the slope of the line between those points repeat the process for two different ordered pairs

Answer 1

From the graph we identify 4 points

`\begin{gathered} (0,7)\to P1 \\ (1,7.5)\to P2 \\ \mleft(2,8\mright)_{}\to P3 \\ (3,8.5)\to P4 \end{gathered}`

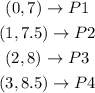
To find the ratio we use the following equation

`m=(y_2-y_1)/(x_2-x_1)_{}`

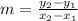
We plug in the values of the chosen points (P1 and P2) to find the slope:

`\begin{gathered} m_(1,2)=(7.5-7)/(1-0) \\ m_(1,2)=(0.5)/(1) \\ m_(1,2)=0.5 \end{gathered}`

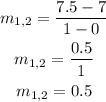
Now, we find the slope for another pair of points (P3 and P4)

`\begin{gathered} m_(3,4)=(8.5-8)/(3-2) \\ m_(3,4)=(0.5)/(1) \\ m_(3,4)=0.5 \end{gathered}`

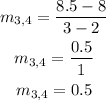
We can observe that the rate of change is constant for all points obtaining a slope of 0.5