Given,
The expression of the function f(x) is 2/5 x + 1/3.
The expression of the function g(x) is 5/2 x - 5/6.
Required
To identify whether the function are inverse of each other.
The function is inverse of each other when f(g(x)) = x and g(f(x)) = x.
So,
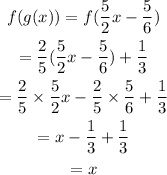
Checking for g(f(X)).
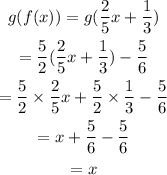
Hence, both the function are inverse of each other.