Question

The Drama Club receives $5769 by selling 576 tickets tothe opening night of the revue. If the full price of a ticket is $12.75and discount tickets for students and seniors are $7.50 each, howmany discounted senior/student tickets were sold?

Answer 1

We have two variables the amount of full price tickets, we call x, and the discounted tickets, we call y.

From the problem, we know the total amount of tickets, 576=x+y, and the total money for the sales $5769, and the prices fro full ticket is $12.75 and for discounted ticket is $7.50.

So the equations are:

`\begin{gathered} \text{The total amount of tickets:} \\ x+y=576 \\ \text{The total money:} \\ 12.75\cdot x+7.5\cdot y=5769 \end{gathered}`

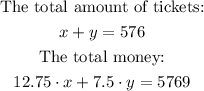
Solving the above system of equations:

`\begin{gathered} y=576-x \\ 12.75\cdot x+7.5\cdot(576-x)=5769 \\ 12.75\cdot x-7.5\cdot x+7.5\cdot576=5769 \\ (12.75-7.5)\cdot x+4320=5769 \\ 5.25\cdot x=5769-4320=1449 \\ x=(1449)/(5.25)=276 \\ y=576-276=300 \end{gathered}`

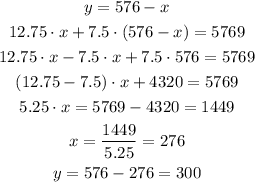
So, were sold 300 dicounted senior/student tickets