Question

m> ma- A diThe mean distance of a moon from a planet is 2.5x10° miles. Assuming that the orbit of the moon around the planet is circular with 1 revolution taking 29.8 days and1 day on this planet taking 22 hours, find the linear speed of the moon. Express your answer in miles per hour.14 cm

Answer 1

Circular Motion

When a body has a uniform circular motion, its distance to a fixed point is always the same and it travels at equal angles in equal amounts of time.

We are given the equation of a circle as:

`y^2+x^2=r^2`

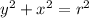
Where x is the horizontal distance and y is the vertical distance. The parametric equations for this motion are:

x = r cos θ

y = r sin θ

Differentiating with respect to time:

x' = -r sin θ θ'

y' = r cos θ θ'

Where θ' is the angular speed. The linear speed is defined as:

`v=\sqrt[]{x^(\prime)^2+y^(\prime2)}`

Substituting:

`v=r\theta^(\prime)`

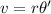
The angular speed is the number of radians traveled per unit of time.

The moon travels 29.8 days of 22 hours each per revolution, that is,

29.8*22 = 655.6 hours per revolution. The angular speed is:

`\theta^(\prime)=(2\pi)/(655.6)=0.0095839\text{ rad/h}`

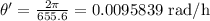
Finally, the linear speed is:

`\begin{gathered} v=2.5\cdot10^5\cdot0.0095839 \\ v=2,396\text{ mi/h} \end{gathered}`