Analyze each option to obtain mathematical expressions that model the situation. Then, identify which of them matches the given inequality.
A)
Since the cost to get in is $6 each student, for a number x of students, the cost will be 6x. If they have $80 to spend, then the maximum number of students will be the greatest whole number such that:
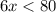
B)
Since Mark will buy a pair of shoes, he will spend at least $30. For a given number x of shirts, he will spend 6x more. In total, he will spend 30+6x to buy x shirts and a pair of shoes. This quantity should be lower than $80:
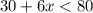
C)
Since the band will earn $6 for each ticket, their total earnings for x tickets would be 6x. Additionaly, they already have $30 and they want to earn a minimum of $80, so the number of tickets must satisfy the condition:
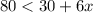
D)
If John works one day and cuts x trees, he will earn 30+6x. If this quantity has to be exactly equal to $80, then x must satisfy the condition:
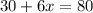
Since the only option that uses the inequality 30+6x<80 is B), that's the only possible answer.