Hello there. To solve this question, we have to remember how to determine the distance between two points in the coordinate plane.
Given two points A = (x0, y0) and B = (x1, y1) in a coordinate plane, using the Pythagoras theorem, is easy to determine that the distance d(A, B) is given by the following expression:
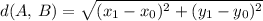
In this case, the points are the coordinates of the mother fox and her kit, given by
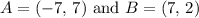
Using the formula, we get
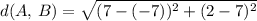
Adding the values inside parenthesis, we get
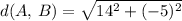
Square and add the numbers
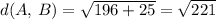
This is the distance between the mother fox and her kit.