first we find the slope with this formula
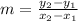
where the point(x2,y2) is the rightmost point between the two points
so, for this case (x2,y2)=(4,8) and (x1,y1)=(3,4)
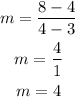
and the general equation of a line is
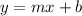
we can find b replace the points(x,y) with any point of the line, example (3,4)
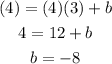
next, make the equation with b and m
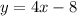
you can replace a point to chek
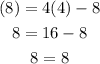
so, correct