Let's draw a picture of our triangle:
We know that the larger acute angle is always in front of the large leg (denoted by x). So, we can relate the unknown angle with the shorter leg and the hypotenuse by means of the cosine function, that is,
![\cos \theta=\frac{\text{ adjancent leg to theta}}{\text{hypotenuse}}=\frac{2\sqrt[]{6}}{2\sqrt[]{15}}](https://img.qammunity.org/2023/formulas/mathematics/high-school/v8gwzr9vtc8cicslr1qp5mb6zdtwqks7ol.png)
which gives
![\begin{gathered} \cos \theta=\frac{\sqrt[]{6}}{\sqrt[]{15}}=\frac{\sqrt[]{2*3}}{\sqrt[]{5*3}} \\ \cos \theta=\frac{\sqrt[]{2}}{\sqrt[]{5}} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/pafgn3iealt5xchifg04lq381c13amnyx7.png)
Then, we have
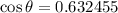
Now, by applying the respective inverse function, we have
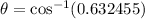
which gives
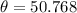
Therefore, by rounding the nearest tenth, the answer is 50.8 degrees