Question

2 numbers whose sum is 15. 3 times one number is 11 less than 5 times the other

Answer 1

Define the variables involved in the situation, which are x and y.

According to the statement, the sum of x and y is 15, this is:

`x+y=15`

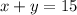
It is also said that 3 times one number, this is 3x, is 11 less than 5 times the other, this is 5y-11.

`3x=5y-11`

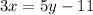
Solve the system formed by these equations:

`\begin{gathered} x+y=15 \\ 3x=5y-11 \end{gathered}`

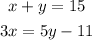
Use equalization method to solve the system, to do this, solve both equations for one of the variables and then make them equal:

`\begin{gathered} x=15-y \\ x=((5y-11))/(3) \\ 15-y=((5y-11))/(3) \\ 45-3y=5y-11 \\ 45+11=5y+3y \\ 56=8y \\ (56)/(8)=y \\ y=7 \end{gathered}`

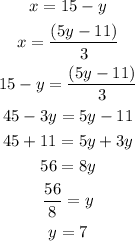
y has a value of 7. Use this value and one of the equations above to find the value of x:

`\begin{gathered} x+y=15 \\ x+7=15 \\ x=15-7 \\ x=8 \end{gathered}`

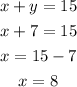
x has a value of 8.

The numbers are 7 and 8.