Question

The circuit below is a combination circuit. The resistance values are R1 = 4 Ω R2 = 4 Ω R3 = 2 Ω Determine the equivalent resistance (for the combination of three resistors), the voltmeter readings and the ammeter readings at the indicated locations.Req = ----- Ω V1 = ------- VV3 = ------ V I1 = ----- A I2 = ----AI3 = ----- A

Answer 1

`\begin{gathered} R_(eq)=4Ω \\ \\ V_1=V_2=6V \\ \\ V_3=6V \\ \\ I_1=1.5A \\ \\ I_2=1.5A \\ \\ I_3=3A \end{gathered}`

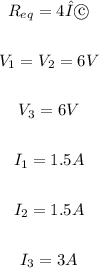
Step-by-step explanation

First, we have to find the equivalent resistance of the circuit:

`R=(1)/(((1)/(R_1)+(1)/(R_2)))+R_3`

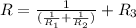
Substitute the values of R1, R2, and R3 to solve for R:

`\begin{gathered} R=(1)/(((1)/(4)+(1)/(4)))+2 \\ \\ R=(1)/((1)/(2))+2=2+2 \\ \\ R=4Ω \end{gathered}`

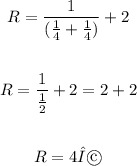
The net current passing through the circuit can be found by applying Ohm's law:

`I=(V)/(R)`

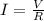
where V = total voltage; R = equivalent resistance

Therefore, the total current passing through the circuit is:

`\begin{gathered} I=(12)/(4) \\ \\ I=3Ω \end{gathered}`

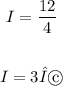
The voltage at R1 and R2 will be equal since the two resistors have the same resistance. This implies that the voltage at R1 is:

`\begin{gathered} V_1=V_2=I((R_1)/(2)) \\ \\ V_1=V_2=(3*4)/(2)=6V \end{gathered}`

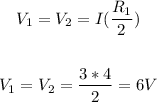
The total current in the circuit flows through R3, so the voltage at V3 is:

`\begin{gathered} V_3=IR_3 \\ \\ V_3=3*2 \\ \\ V_3=6V \end{gathered}`

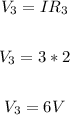
The current flowing through R1 and R2 are equal. Since the two resistors are in parallel and have an equal value, the current flowing through R1 and R2 is half the current flowing through the circuit:

`I_1=I_2=(3)/(2)=1.5A`

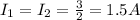
and as explained above:

`I_3=3A`