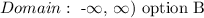Answer:
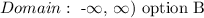
Step-by-step explanation:
Given:
f(x) = 4x + 12
g(x) = x + 2
To find:
f ∘ g
To determine f ∘ g, we will substiute x in f(x) with function g(x)
![\begin{gathered} f∘g\text{ = \lparen f \circ g\rparen\lparen x\rparen} \\ (f∘g)(x)\text{ = f\lparen g\lparen x\rparen\rparen} \\ \\ f(g(x))\text{ = 4\lparen x + 2\rparen + 12} \\ f(g(x))\text{ = 4x + 8 + 12} \\ f\mleft(g\mleft(x\mright)\mright)\text{ = 4x + 20} \\ \\ f∘g\text{ = 4x + 20} \end{gathered}]()
Domain are the inputs (x values) of a function
The function f ∘ g = 4x + 20 does not have a restriction on the x values. x can take on any number
Hence, the domain of f ∘ g is all real number