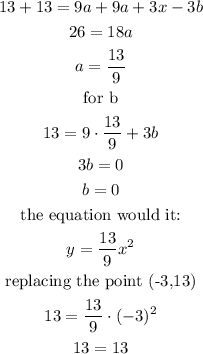Question

Create a quadratic function that has a solution at (-3, 13). Demonstrate that your function has thissolution.

Answer 1

`\begin{gathered} y=\sqrt[]{178-x^2} \\ or \\ y=(13)/(9)x^2 \end{gathered}`

Explanation:

In the case that (-3, 13) is a point (x, y), the answer is the following:

The way to solve this problem is through trial and error.

In this case, we can propose the following quadratic equation:

`y=√(178-x^2)`

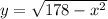
We check the equation by replacing in the function:

`\begin{gathered} y=\sqrt[]{178-(-3)^2} \\ y=\sqrt[]{178-9} \\ y=\sqrt[]{169} \\ y=\pm13 \end{gathered}`

Therefore, the point (-3, 13) is part of the solution of the proposed function

Or we can opt for the 3-point method:

For (0, 0) we have

0 = C

For (3, 13) we have

13 = 9a + 3b

For (-3, 13) we have

13 = 9a - 3b

adding them:

`\begin{gathered} 13+13=9a+9a+3x-3b \\ 26=18a \\ a=(13)/(9) \\ \text{for b} \\ 13=9\cdot(13)/(9)+3b \\ 3b=0 \\ b=0 \\ \text{the equation would it:} \\ y=(13)/(9)x^2 \\ \text{replacing the point (-3,13)} \\ 13=(13)/(9)\cdot(-3)^2 \\ 13=13 \end{gathered}`