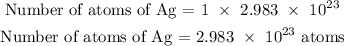ANSWER
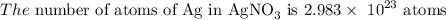
Step-by-step explanation
Given information
The mass of silver nitrate (AgNO3) = 84.15 grams
Avogadro's constant = 6.022 x 10^23
To find the number of atoms of AgNO3, follow the steps below
Step 1: Find the number of moles using the below formula
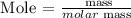
Recall, that the molar mass of AgNO3 is 169.87 g/mol
Step 2: Substitute the given data into the formula in step 1
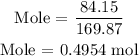
Hence, the number of moles of AgNO3 is 0.4954 mole
Step 3: Find the number of atoms of AgNO3 using the formula below
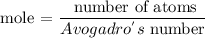
Let the number of atoms be x

Since we have 1 atom of Ag in AgNO3, hence, the number of atoms of Ag in AgNO3 is calculated below