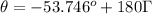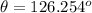Question

A vector A has components Ax = −5.50 m and Ay = 7.50 m. Find the magnitude (in m) and the direction (in degrees counterclockwise from the +x-axis) of the vector.What is the direction?

Answer 1

Vectors

Given a vector of components A = (Ax, Ay), the magnitude of the vector is:

`|A|=\sqrt[]{A^2_x+A^2_y}`

And the angle in standard form (counterclockwise from the positive x-direction is given by:

`\tan \theta=(A_y)/(A_x)`

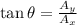
The vector A has components Ax = -5.50 m and Ay = 7.50 m. The magnitude is calculated as follows:

`\begin{gathered} |A|=\sqrt[]{(-5,50)^2+7.50^2} \\ \text{Operating:} \\ |A|=\sqrt[]{30.25+56.25} \\ |A|=\sqrt[]{86.5} \\ |A|=9.3 \end{gathered}`

The magnitude of A is 9.3 m.

Calculate the angle. It's important to notice the x-coordinate is negative and the y-coordinate is positive, thus the angle is in quadrant II (between 90° and 180°).

`\tan \theta=(7.50)/(-5.50)=-1.3636`

Calculating the angle with the inverse tangent function:

`\theta=-53.746^o`

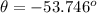
This angle is not expressed correctly in the second quadrant, so we have to add 180°:

`\theta=-53.746^o+180\~`
`\theta=126.254^o`