Question

graph y= x² + 2x - 8. Then determine which answer choice matches the graph you drew. Find the x-intercepts.Identify the solution that has the correct graph and the correct x-intercepts.

Answer 1

Option A

Step-by-step explanation

First, we have to find the x-intercepts, so we have to solve,

`x^2+2x-8=0`

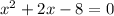
To do so, we can use the quadratic formula,

`\begin{gathered} ax^2+bx+c=0 \\ x=(-b\pm√(b^2-4ac))/(2a) \end{gathered}`

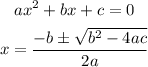
In this case, a = 1, b = 2, and c = -8,

`x=(-2\pm√(2^2-4\cdot1\cdot(-8)))/(2\cdot1)=(-2\pm√(4+32))/(2)=(-2\pm√(36))/(2)=(-2\pm6)/(2)`

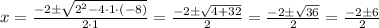
So, the x-coordinates of the two x-intercepts are,

`\begin{gathered} x=(-2-6)/(2)=(-8)/(2)=-4 \\ \\ x=(-2+6)/(2)=(4)/(2)=2 \end{gathered}`

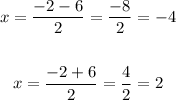
Hence, the x-intercepts are (-4, 0) and (2, 0), which reduces the graph options to two possibilities: graph A or graph C. Each has the x-coordinate of its vertex at each side of the y-axis: for graph A the x-coordinate of the vertex is negative, while for graph C it is positive.

To decide which one of these graphs is the correct one, we will find the x-coordinate of the vertex of the function, given by,

`x_(vertex)=(-b)/(2a)`

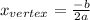
In this case, a = 1, and b = 2,

`x_(vertex)=(-2)/(2\cdot1)=-1`

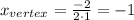
Hence, the graph of this function is graph A.