Question

Tiffany has 31 coins in her pocket, all of which are dimes and quarters. If the total value of her changeis $5.65, how many dimes and how many quarters does she have?Number of dimes that Tiffany has =Number of quarters that Tiffany has =

Answer 1

Given:

The number of coins, N=31.

The total value of the coins, T=$5.65.

Let x be the number of dimes and y be the number of quarters.

The equation for the number of coins can be expressed as,

`x+y=31-----(1)`

We know,

1 dollar=100 cents.

Hence, 1 cent is,

`1\text{ cent=}(1)/(100)dollar`

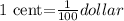
1 quarter=25 cents.

Then, 1 quarter in dollars is,

`1\text{ quarter =25 cent=25}*(1)/(100)dollar=0.25\text{ dollar}`

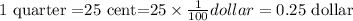
1 dime=10cents.

Then, 1 dime in dollars is,

`1\text{ dime=1}0\text{ cents}=10*(1)/(100)dollar=(1)/(10)dollar=0.1\text{ dollar}`

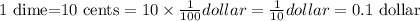
Now, the equation for the total value of coins can be expressed as,

`\begin{gathered} 0.1x+0.25y=T \\ 0.1x+0.25y\text{ =5.65------(2)} \end{gathered}`

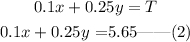
Multiply equation (1) by 0.1.

`0.1x+0.1y=3.1\text{ ------(3)}`

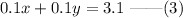
Now, subtract equation (3) from (2) to find the value of y.

`\begin{gathered} 0.1x+0.25y-0.1x-0.1y\text{ =5}.65-3.1 \\ 0.15y=2.55 \\ y=(2.55)/(0.15) \\ y=17 \end{gathered}`

Now, put y=17 in equation (1) to find the value of x.

`\begin{gathered} x+17=31 \\ x=31-17 \\ x=14 \end{gathered}`

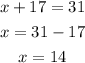
Therefore, the number of dimes is 14 and the number of quarters is 17.