Question

Find the coordinates of the intersection of the diagonals of parallelogram QRST with verticesQ(-8, 1), R(2, 1), S(4,-3), and T(-6,-3).The coordinates of the intersection are

Answer 1

Lets draw the parallelogram:

Since diagonals QS and RT divide each other into segments of equal lenght, the diagonal bisect each other.

This means that the intersection point A is the middle point of segment QS (or TR). Therefore, we need to compute the middle point of one of segment.

The middle point formula is

`A=((x_1+x_2)/(2),(y_1+y_2)/(2))`

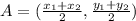
where

`\begin{gathered} T=(x_1,y_1)=(-6,-3) \\ R=(x_2,y_2)=(2,1) \end{gathered}`

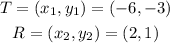
By substituting these values into the middle point formula ,we get

`A=((-6+2)/(2),(-3+1)/(2))`

which gives

`\begin{gathered} A=((-4)/(2),(-2)/(2)) \\ A=(-2,-1) \end{gathered}`

Therefore, the coordinates of the intersection points are (-2, -1).