Question

A circle has a diameter with endpoints at (18, -13) and (4, -3).

Answer 1

`(x-11)^2+(y+8)^2=74`

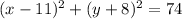
Step-by-step explanation

Given:

A circle with endpoints (18, -13) and (4, 3) as the diameter.

Desired Outcome:

Equation of the circle.

Determine the center of the circle using the midpoint formula

`((x_1+x_2)/(2),(y_1+y_2)/(2))`

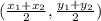
where:

x1 = 18

x2 = 4

y1 = -13

y2 = -3

Substitute the values:

`\begin{gathered} ((18+4)/(2),(-13-3)/(2)) \\ =((22)/(2),(-16)/(2)) \\ =(11,-8) \end{gathered}`

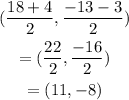
Therefore, the center (h, k) of the circle is (11, -8)

Determine the radius of the circle

`r=√((x_2-x_1)^2+(y_2-y_1)^2)^`

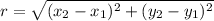
where:

x1 = 11

x2 = 4

y1 = -8

y2 = -3

Substitute the values:

`\begin{gathered} r=√((4-11)^2+(-3--8)^2)^ \\ r=√((-7)^2+(-5)^2) \\ r=√(49+25) \\ r=√(74) \end{gathered}`

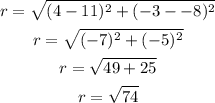
Now, the equation of the circle is:

`\begin{gathered} (x-h)^2+(y-k)^2=r^2 \\ (x-11)^2+(y--8)^2=(√(74))^2 \\ (x-11)^2+(y+8)^2=74 \end{gathered}`

Graph: