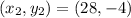We are given the midpoint and one endpoint of a line segment.
Midpoint = (10, -7)
Endpoint = (-8, -10)
We are asked to find the other endpoint.
Recall that the midpoint formula is given by
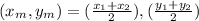
Let us solve for the other endpoint (x₂, y₂)
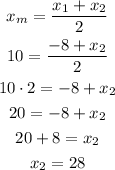
Similarly,
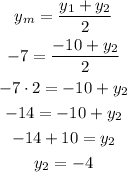
Therefore, the other endpoint is