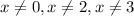SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Write the given expression
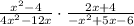
STEP 2: State the condition for knowing the restricted values
The restricted values for rational expressions are based on the fact that you cannot divide by zero, so you must restrict any value for any variable in the denominator of a rational expression that would make the value of the denominator be zero. That's how you solve Restricted Values.
STEP 3: Simplify the given expression

STEP 4: Equate the product to zero and solve for x
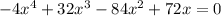
Using graphical method,
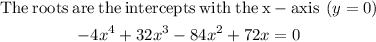
Getting the x-intercepts,
Hence, the answer is given as: