From the information given in the statement, you know that the baker is going to use 11 cups to prepare his cookies, because
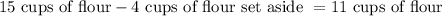
Now, to find out how many batches of cookies the baker can make with 11 cups of flour, you can use the following ratio:

Since
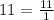
then when dividing the fractions you have
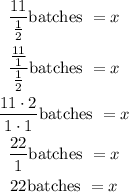
Therefore, the baker can make 22 cookie batches with 11 cups of flour.