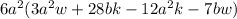We have the following expression:
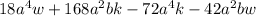
Lets find the greatest common factor of all terms. We can note that the gcf of the number is

They have in common the number 6, then we can rewritte our expression as:
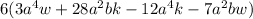
Regarding the variables, we can note that the term
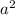
is in all the terms of our expression, then we have