Let the first(smaller) number = x
Let the other(larger) number= y
One number is four times the other number.
• y=4x
If 6 is added to the smaller number, we have: x+6
If 4 is added to the larger number, we have: y+4
Then the later number becomes twice the other number
• The later number = y+4
Therefore:
y+4=2(x+6)
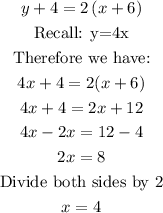
Next, we substitute x=4 to find the value of y
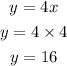
The numbers are 4 and 16.