Question

David reads 40 pages of a book in 60 minutes. How many pages should he be able to read in 90 minutes if he reads at a constant rate?

Answer 1

The formula for Rate is given below as,

`\text{Rate}=(Volume)/(Time)`

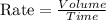
If David reads 40 pages of a book in 60 minutes, the rate will be,

`\begin{gathered} \text{Volume}=40\text{pages} \\ \text{Time}=60\min \\ \text{Rate}=(40)/(60)=(2)/(3) \end{gathered}`

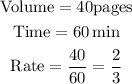
If the rate is constant (i.e he reads at a constant rate), the number of pages he should be able to read in 90 mins will be,

`\begin{gathered} \text{Rate}=(Volume)/(Time) \\ \text{Where Rate =}(2)/(3) \\ \text{Time=90mins} \\ (2)/(3)=(Volume)/(90) \\ \text{Crossmultiply} \\ 3* Volume=2*90 \\ \text{Divide both sides by 3} \\ \text{Volume}=(2*90)/(3)=60\text{ pages} \end{gathered}`

Hence, he should be able to read 60 pages if he reads at a constant rate.