Question

a private airplane leaves an airport and flies due south at 192 km per hour. two hours later a jet leaves the same airport and flies due south at 960 km per hour. when will the jet overtake the plane?

Answer 1

Data:

Airplane: 192km/h

Jet: 960kn/h

1. Calculate the distance traveled by the airplane in the 2 hours before the jet leaves the airport:

Multiply the speed by 2:

2. Write an equation for the distance traveled for airplane (A) after 2 hours it leaves airport and other equation for the distance traveled for jet (J) since it leaves the airport:

`\begin{gathered} A=192t+384 \\ \\ J=960t \end{gathered}`

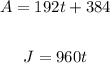
t is the time in hours

3. Write an inequality to J greather than A (it is the moment the jet overtake the airplane)

`\begin{gathered} J>A \\ \\ 960t>192t+384 \end{gathered}`

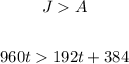
4. Solve the inequality:

-Substract 192t in both sides of the inequality:

`\begin{gathered} 960t-192t>192t-192t+384 \\ 768t>384 \end{gathered}`

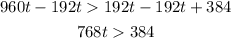
-Divide both sides of the inequality by 768:

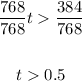
`\begin{gathered} (768)/(768)t>(384)/(768) \\ \\ t>0.5 \end{gathered}`Then, after 0.5 hours (30 minutes) the jet overtakes the airplane