Given the ratios:
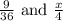
Let's find the value of x that makes each pair of ratios equivalent.
Equivalent ratios are ratios that have the same value.
To find the value of x, let's equate both ratios and solve for x.
We have:

Therefore, the value of x that makes the pair of ratios equivalent is 1
ANSWER:
1