Question

What is the equation of a circle whose diameter endpoints are at (-6, -12) and (4, -10)

Answer 1

Endpoints of the diameter: (-6, -12) and (4, -10)

1. Find the coordinates of the center: The center is the midpoint of the diameter.

Use the midpoint formula to find the center of the circle:

`((x_1+x_2)/(2),(y_1+y_2)/(2))`
`\begin{gathered} ((-6+4)/(2),(-12-10)/(2)) \\ \\ (-(2)/(2),-(22)/(2)) \\ \\ (-1,-11) \end{gathered}`

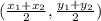
Center of the circle (-1,-11)

2. Find the radius of the circle: as the radius is the distance from the center of the cirlce to any point on its circumference, use the formula for distance between two points to find the distance between (-1,-11) to (-6,-12):

`d=\sqrt[]{(x_2-_{}x_1)^2+(y_2-y_1)^2}`
`\begin{gathered} r=\sqrt[]{(-1-(-6))^2+(-11-(-12))^2} \\ \\ r=\sqrt[]{5^2+1^2} \\ \\ r=\sqrt[]{25+1} \\ \\ r=\sqrt[]{26} \end{gathered}`

3. Use center (h,k) and radius (r) to write the equation of the circle:

`(x-h)^2+(y-k)^2=r^2`
`\begin{gathered} (x-(-1))^2+(y-(-11))^2=(\sqrt[]{26})^2 \\ \\ (x+2)^2+(y+11)^2=26 \end{gathered}`

Then, the equation of the given circle is:

`(x+2)^2+(y+11)^2=26`