EXPLANATION
Let's see the facts:
Number of bees = 1500
Decreasing rate = 12% = 0.12 (in decimal form)
Number of flowering plants = 800
Number of removed plants/month = 25
Part A:
Function for the number of bees:
y = a (1-r)^x
Where a= initial population = 1500 r=decay rate in decimal form
Replacing terms:
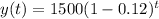
Function for the number of flower plants throughout the months.
In this case, we know to consider that there is a decreasing of 25 plants by month:
g (t)= 800 -25t
Part B:
After 6 months, we would have,
#Bees:
y(6) = 1,500(0.88)^6
= 1,500*0.46
= 696 bees
#Plants:
g(6) = 800 - 25*6
= 800 - 150
= 650 flowering plants
Part C:
Here we need to equal both equations:
y(t)= 1,500*(0.88)^t= 800 - 25t = g(t)
We can plug differents values of t until both equations are equal.
#5
1,500*(0.88)^5= 800 - 25*5
791.59 > 675
#6
1,500*(0.88)^6= 800 - 25*6
696.6 > 675
#7
1,500*(0.88)^6= 800 - 25*6
613 < 675
The solution is between 6 and 7. Let's try with 6.5 months:
1,500*(0.88)^6.5= 800 - 25*6
653 < 675
Thus, the solution is greater than 6.5 but smaller than 7. Hence, we can affirm that the number of months is equal to 7.