Given:
The expression is:
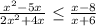
Find-:
Solve the expression
Explanation-:
The expression is:
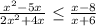
The value of "x" is:
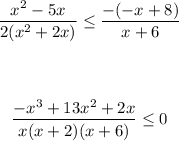
So, the "x" is:
The factor is:
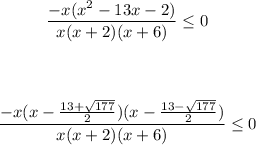
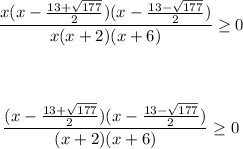
The "x" in interval is:
[tex]\begin{gathered} \frac{(x-\frac{13+\sqrt{177}}{2})(x-\frac{13-\sqrt{177}}{2})}{(x+2)(x+6)}\ge0 \\ \\ x<-6\text{ or }-2Is the value for "x"