First we have to find the profit function P(x).
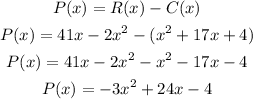
The maximum value of the quadratic function is the vertex as it opens downward. Finding the vertex, we have:
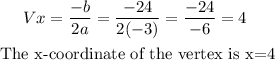
We see that the number of units needed to maximize the profit is 4 units and it satisfies the condition of being between 0 and 13 units.
The answer is x=4.