Given
The function
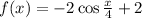
To find the time at which the pendulum is 4 meters away from its starting point.
Now,
Let x be the time at which the pendulum moves.
Let f(x) be the distance of the pendulum from its starting point at time x.
Then,
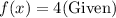
Therefore,
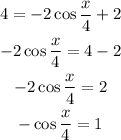
Since
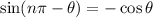
Then,
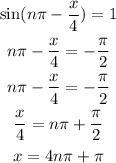
Hence, the answer is option c).