Question

How far along the ladder can a 750 N person climb up the ladder?

Answer 1

We will ahve the following:

Forces on x:

`\sum ^{}_{}F_x=0=\sigma-n_1\colon\sigma=n_1`

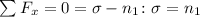
Forces on y:

`\sum ^{}_{}F_y=0=n_2-200N-750N\colon n_2=950N`

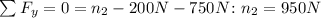
Since it is a stable system we will have:

`n_1=\mu n_1`

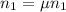
Now, we will determine the torque at the bottom of the ladder:

`\sum ^{}_{}\tau_{\text{bottom}}=0-(200N)(3m)\cos (56)`

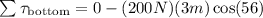
Also:

`-(750N)(d)\cos (56)`

&

`+(n_1)(5m)\sin (56)`

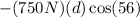
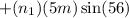
Finally:

`0=-600\cos (56)-d\cdot750\cos (56)+(285)(5)\sin (56)\Rightarrow-d\cdot750\sin (56)=600\cos (56)-(285)(5)\sin (56)`
`\Rightarrow d=((285)(5)\sin (56)-600\cos (56))/(750\cos (56))\Rightarrow d=2.01686584`
`\Rightarrow d\approx2.02`

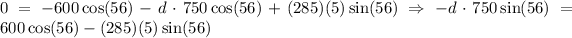
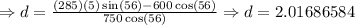
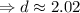
So, the distance along the ladded that a 750N person could climb in the ladder would be approximately 2.02 meters.