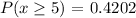The flight is either early or late. Since these are the only outcomes, this is a binomial probability. The formula for determining binomial probability is expressed as
P(x) = nCx * p^x * q^(n - x)
where
n = number of trials
x = number of successes
p = probability of success
q = probability of failure
The success in this case is the outcome of the flight being on time. Thus, we have
n = 6
p = 70/100 = 0.7
q = 1 - p = 1 - 0.7 = 0.3
For the probability that exactly 4 flights our own time is on time,
x = 4
Thus
P(x = 4) = 6C4 * 0.7^4 * 0.3^(6 - 4)
P(x = 4) = 0.3241
From the binomial distribution calculator, the probability of at most 3 flights is
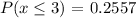
From the binomial distribution calculator, the probability of at least 5 flights is