The points given:
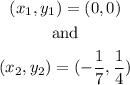
The slope, m, of the line can be found using the slope formula:

Substituting the points, we get:
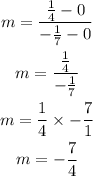
The slope intercept form of a line is y = mx + b
We can now write:
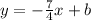
We know, (0,0) is a point, so we substitute it and find b:

The equation is:
