We will use the next diagram
Where Fr, is the frictional force, F is the applied force, W is the weight and N is the normal
For a)
We analyze the horizontal forces
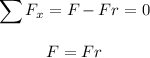
Then we analyze the vertical forces
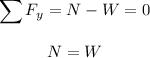
then for the frictional force
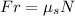
Then for the force we have
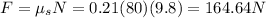
Then for b)
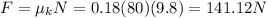
We