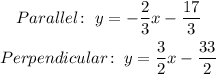Question

Consider the line with the equation: y = - 2 - 2 - 3 3 Give the equation of the line parallel to Line 1 which passes through (5, – 9): Give the equation of the line perpendicular to Line 1 which passes through (5, – 9):

Answer 1

We are given the following equation of a line

`y=-(2)/(3)x-3`

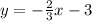
Give the equation of the line parallel to line 1 which passes through (5, -9)

Recall that the standard form of the equation of a line in slope-intercept form is given by

`y=mx+b`

Where m is the slope and b is the y-intercept.

Comparing the standard form with the given equation we see that the slope of line 1 is -2/3

Since we are given that the lines are parallel so the slope of the other line must be equal that is -2/3

So, the equation of the other line becomes

`y=-(2)/(3)x+b`

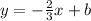
To find the value of b, substitute the point (5, -9) into the above equation and solve for b.

`\begin{gathered} -9=-(2)/(3)(5)+b \\ -9=-(10)/(3)+b \\ -9+(10)/(3)=b \\ -(17)/(3)=b \\ b=-(17)/(3) \end{gathered}`

So, the equation of the other line is

`y=-(2)/(3)x-(17)/(3)`

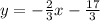
Give the equation of the line perpendicular to line 1 which passes through (5, -9)

Since we are given that the lines are perpendicular so the slope of the other line must be negative reciprocal of the given line.

`m_2=-(1)/(m_1)=-(1)/(-(2)/(3))=(3)/(2)`

So, the slope of the other line is 3/2

The equation of the other line becomes

`y=(3)/(2)x+b`

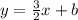
To find the value of b, substitute the point (5, -9) into the above equation and solve for b

`\begin{gathered} -9=(3)/(2)(5)+b \\ -9=(15)/(2)+b \\ -9-(15)/(2)=b \\ -(33)/(2)=b \\ b=-(33)/(2) \end{gathered}`

So, the equation of the other line is

`y=(3)/(2)x-(33)/(2)`
`\begin{gathered} Parallel\colon\; y=-(2)/(3)x-(17)/(3) \\ Perpendicular\colon\; y=(3)/(2)x-(33)/(2) \end{gathered}`