Question

How many solutions does this system of equations have( one, no, infinitely many){y+2/3x=4{2x=12-3y

Answer 1

The system has infinitely many solutions

Step-by-step explanation:

We will try to solve the system, so:

If we isolate y on the first equation, we get:

y = 4 - (2/3)x

So, replacing y on the second equation and solving for x, we get:

`\begin{gathered} 2x=12-3y \\ 2x=12-3(4-(2)/(3)x) \\ 2x=12-(3\cdot4)+(3\cdot(2)/(3)x) \\ 2x=12-12+2x \\ 2x=2x \end{gathered}`

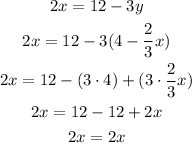
Since we get an identity, the system of equations has infinitely many solutions.